Мета:  Узагальнити вивчене на попередніх уроках. Перевірити набуті знання, уміння і навички учнів по даній темі

Обладнання: Інтерактивна дошка, роздатковий матеріал, плакати

«Кожне наукове відкриття дає рішення великої проблеми, але й

у розв’язанні  задачі є дрібка відкриття»

(Д. Пойя, американський математик)

Тип уроку: Узагальнення вивченого матеріалу, підведення підсумків

ХІД УРОКУ

І. Організаційний етап.

ІІ. Перевірка Д/З

Два учні доводять творчі завдання

1. Довести що площа квадрата побудованого на гіпотенузі, дорівнює сумі площ квадратів побудованих на катетах  прямокутному трикутнику.
2. Довести теорему Піфагора за подібністю трикутників.
3. Розв’язати вправу «Незакінчені речення»

• Сума гострих кутів прямокутного трикутника дорівнює (90 градусів);
• Гіпотенуза в прямокутному трикутнику більша (катета);
• Квадрат гіпотенузи дорівнює (сумі квадратів катетів);
• Якщо з даної точки до прямої проведено перпендикуляр і похилі, то будь-яка похила (більша від перпендикуляра)
• Якщо до прямої з однієї точки проведені перпендикуляр і похилі, то рівні похилі (мають рівні проекції );
• Відрізок який сполучає основу перпендикуляра і похилої називається (проекцією)
• Якщо до прямої з однієї точки проведені дві похилі, то більша та , у (якої проекція більша)
• Якщо квадрат гіпотенузи дорівнює сумі квадратів катетів, то цей трикутник (прямокутний)

4. Понад 100 способів доведення теореми Піфагора,подивіться деякі з них:

а) на основі мозаїки побудованої із рівнобедрених прямокутних трикутників

б) В Індії був свій спосіб доведення загального випадку за побудовою двох квадратів спочатку на катетах а потім на гіпотенузах тих самих прямокутних трикутників

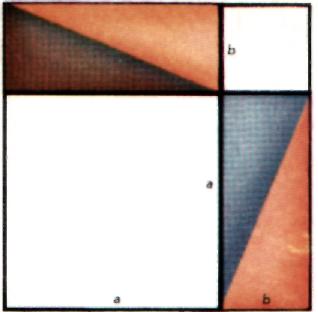
в) За сумою пів площ кругів побудованих на сторонах прямокутного трикутника , як на діаметрах (цей спосіб запропонував давньогрецький математик Гіппократ)

г)в наші дні в доведення теореми Піфагора було покладено побудову квадратів на сторонах прямокутного трикутника

ІІІ. Формулювання теми, мети і завдань уроку.

Запропонувати учням висловити мету уроку.»Сьогоднішній урок навчить мене знаходити невідомі елементи в прямокутному трикутнику, використовуючи теорему Піфагора»

ІV. Актуалізація опорних знань і умінь.

Знайти невідомий елемент у прямокутних трикутниках.

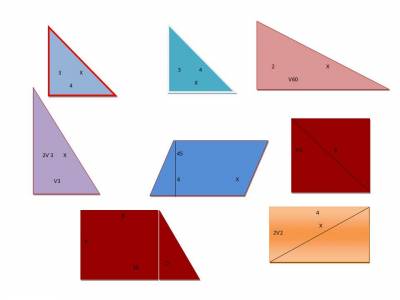
V.  Розв’язання вправ і задач. Самостійна робота.

1. Обчислити периметр прямокутника, якщо одна сторона 5Н см а друга 13Н см (24Н)

2. Основа рівнобедреного трикутника 16Н см, а висота, проведена до основи 6Н см. Знайти бічну сторону трикутника (10Н)

3. Обчислити бічну сторону рівнобедреної трапеції, якщо її основа дорівнює Нсм і 13Н см а висота рівна 8Н см (10Н)

4. Діагоналі ромба 6Н і  8Н см. Обчислити периметр ромба (20Н)

5.  АВСД ромб, точка О – точка перетину діагоналей, ВС=5 см, ОС=3 см. Знайти ВД (ВД=8 см)

6 . Гіпотенуза рівнобедреного трикутника дорівнює 26 см. А катети відносяться як 5:12. Знайти катети цього трикутника. (10 см і 24 см)

VІ.  Підсумок уроку.

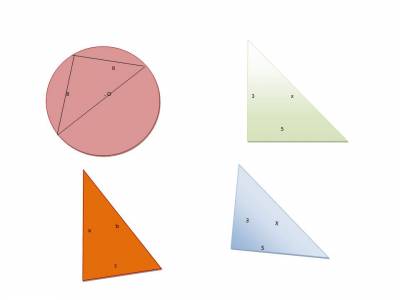
1. На що слід звернути увагу під час застосування теореми Піфагора?

(теорема Піфагора застосовується лише для розв’язання  прямокутних трикутників)

2. Як ви вважаєте, де можна застосувати отримані знання та навички у житті? (під час проектування конструкцій технічного та побутового характеру)

VI. Домашнє завдання Повторити § 23, 24 №9 (б, г), №7, Скласти кросворд, задачу.